Numerische Berechnung von Integralen (Flächen)

Graphische Darstellung der Kepler´sche Fassregel am Beispiel



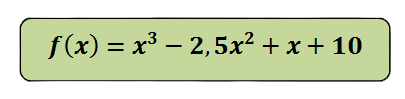
Bei der numerische Berechnung des Flächenintegrales nach Kepler wird die zu integrierende Funktion durch eine Funktion 2. Grades, hier die blaue Funktion g(x), ersetzt. Deren Fläche lässt sich mit folgender Formel bestimmen:


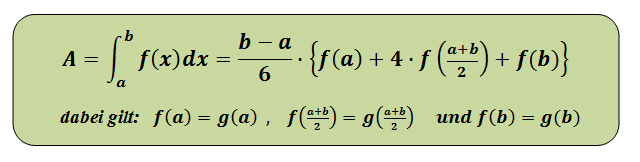
Du kannst die beiden Integralgrenzen (Punkte auf der x-Achse) mit Hilfe der gedrückten linken Maustaste verschieben. Außerdem kannst Du durch Entfernen der Häkchen oben links Teile der Abbildung unsichtbar bzw. sichtbar machen.



Das ist ein mit GeoGebra www.geogebra.org erstelltes Java-Applet. Möglicherweise ist Java auf Ihrem Computer nicht installiert; bitte besuchen Sie in diesem Fall www.java.com

Dietmar Höckelmann, Erstellt mit GeoGebra


Wie Du hier erkennen kannst, entspricht der mit Hilfe der Kepler´schen Fassregel berechnete Integralwert dem des korrekt berechneten Integrales. Die blaue Ersatzfunktion g(x) muss dabei aber nicht explizit ermittelt werden!

Es werden hier eigentlich nur 3 Funktionswerte berechnet, mit denen man dann nach Kepler (siehe weiter unten) den entsprechenden Integralwert bestimmen kann!!




Hinweis: Die Keplersche Fassregel liefert bei der Berechnung der Integrale von ganzrationalen Funktionen bis zum Grade 3 exakte Werte.