Trigonometrische Funktionen
I. Konstruktion der Sinus und Cosinusfunktion mit Hilfe
des Einheitskreises (r=1)
Für rechtwinklige Dreiecke gelten folgende geometrische Beziehungen:
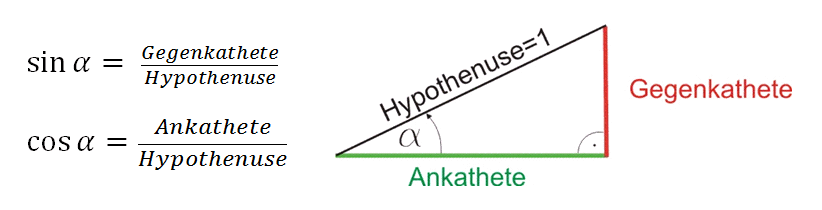
Dieses Dreieck findet man unten in der Konstruktion des Einheitskreises des Applets wieder.
Zur Verdeutlichung der Konstruktion verschiebe den blauen Punkt auf dem Einheitskreis mit Hilfe der Maus.
Dietmar Höckelmann, erstellt mit GeoGebra
Du kannst mit Hilfe der Auswahlkästchen eine oder beide Konstruktionen ein- oder ausschalten.II. Untersuchung der Sinus- und Cosinusfunktionen

Zur Verdeutlichung der Einflüsse der beiden Parameter A, a, b und c der Sinusfunktion sowie B, u, v und w der Cosinus funktion muss Du mit der Maus die Schieberegel der Parameter verschieben.
(zum Löschen der Verschiebespur bitte auf das Symbol oben rechts klicken)
Dietmar Höckelmann, erstellt mit GeoGebra
Durch das Verändern der Koeffizienten der beiden trigonometrischen Funktionen kann man deren Bedeutung leicht erkennen.
Beobachtungen:
A und B = Amplitude der Funktion
a und u = "Streckung bzw. Stauchung der Funktionen in Richtung der x-Achse"
b und v = "Verschiebung der Funktionen in Richtung der x-Achse"
d und w = "Verschiebung der Funktionen auf der Funktionsachse"
Weiteres zum Thema der trionometrischen Funktionen:
Aufgabenbeispiele
Sonstiges